Sokan kétkedve gondolnak arra, hogy a matematika és a művészetek között kapcsolat lehet, mert két különböző alkotói felfogásról van szó. A művészet a fantázia, az érzelmek területe, míg a matematika a logika és a ráció segítségével old meg feladatokat.
Ajánlom a téma iránt érdeklődőknek, hogy nézzünk együtt utána néhány ilyen kapcsolatnak a képzőművészetben, a művészetekben és a természetben, továbbá vizsgáljuk meg, a mai kutatók miképp vélekednek erről a témáról.
Művészettörténeti tanulmányaim során sikerült találkoznom a matematika és az építészet szoros kapcsolatával, ami mindenki számára érthető, hiszen az épületet megtervezik, a tervet felnagyítják, valamint kiszámítják az anyagok ellenállását, hogy az épület tartós legyen. Az ókori Egyiptomból megemlíthetjük Imhotep főpapot, aki a szakkarai lépcsős piramist tervezte, és aki sokoldalú tudós volt: jártas volt az orvostudományban, a matematikában és a csillagászatban is. Az egyiptomiaktól fennmaradt az a képlet, amelyik a piramis élének dőlésszögét szabályozta, és egyben garanciája volt a tartósságnak és esztétikai szépségnek.
A görögök a templomok építésénél modult (moduluszt) használtak, ami az épület részeinek nagyságát határozta meg. Ez a mérték az oszlop aljának sugarával volt egyenlő, valamint a gerendázatban levő triglifek (hármas tagolású díszítő elemek) szélességével. Ez a modul minden épületnél más volt, de egységesítette az épület kivitelezését, biztosította a harmonikus szépséget. A görögök a szobraiknál kánont alkalmaztak, ami a szobor fejének nagyságát jelentette, kiterjesztve az emberalak többi részeire. Így a szobrász, Polükleitosz a szoborfej nagyságát hét és félszer mérte a szoboralakba. Lüszipposznál, egy másik szobrásznál a fejnagyság a szobor nyolcadrészét képezte.
Az antik művészetekben ismert volt az aranymetszés szabálya. A téglalapnál ez a hosszú és rövid oldal arányát 1,618 értékben határozta meg. Az aranymetszést a háromszögre is alkalmazták. Ezzel keresték a harmonikus, szép arányokat.
A reneszánszban az építészek matematikusok is voltak. Így Brunelleschi, aki a firenzei dóm kupoláját tervezte, az építészeten kívül szobrászattal is foglalkozott, valamint matematikai és mérnöki ismeretekkel rendelkezett. Foglalkozott a perspektíva felhasználásával a festészetében – itt ugye a távolodás törvénye jut kifejezésre, miszerint minél távolabbi a tárgy, annál kisebbnek tűnik. A perspektíva több művésznek is felkeltette az érdeklődését, így végül kidolgozták az alkalmazásának lehetőségeit. Az előző korokban az események egy síkban történtek, de ezzel az új szemlélettel az ember valójában a tér részévé vált, beleérezhette magát korának világába.
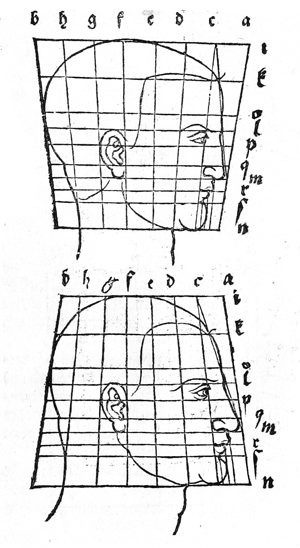
A reneszánsz korának művészei, így Leonardo da Vinci, Albrecht Dürer is tanulmányozta az emberi test arányait – Dürer több könyvet is írt erről a témáról. A reneszánsz, majd az ezt követő barokk kor művészei is nagyméretű kompozíciókat alkottak. Ezeknek a tervezésénél a kompozíciók alakjait valamilyen mértani formában helyezték el. Leonardo da Vinci Sziklás Madonna című képének alakjait háromszög alakba rendezte, ezzel erősítve a kompozíció érzelmi és értelmi hatását. A nagyméretű falfestmények esetében pedig a kicsi tervek felnagyítása mértani beosztással történt.
A barokk kor nagy megvalósítása volt a római Szent Péter tér kialakítása, ami Bernini építész és szobrász műve. Itt olyan számításokat alkalmazott, amivel a bazilika monumentalitását emelte ki, az oszlopsorokkal pedig olyan összhatást ért el, ami az emberekben mély benyomást kelt, különösen a pápai találkozások alkalmával. Korunk nagy emlékművei, térplasztikai alkotásai is matematikai számításokat igényeltek. Gondolok itt a párizsi Eiffel-toronyra, a brüsszeli Atomium emlékműre. Akad olyan szobrász, mint például Nicolas Schöffer, aki nagyméretű tér- és fényszobrokkal gazdagította a városok tereit; de ilyen Calder is az óriási fémszobraival, amelyek igényelték a mérnöki számításokat. Az aranymetszés szabályait korunkban is alkalmazzák – említsük meg például Piet Mondrian konstruktivista művészt, aki a harmonikus, megnyugtató összhatás érdekében ilyen arányokat használt a képein, vagy Le Corbusier építész, aki az aranymetszést és emberi arányokat figyelembe vevő terveket készített.
Vizsgáljuk meg más művészetek esetében, a zenében vagy a költészetben a matematika jelenlétét. Az ókorban a tudósokat a zene is érdekelte. A nagy matematikusok, például Püthagorasz a zenei hangokat hangsorokba szervezték, kialakították az oktávot, ami ma is a zeneszerzés alapjait képezi. A matematika szerepe az, hogy rendszerbe foglalja a hangzásokat, amely így alkalmas lesz különböző zenei kifejezésekre, a zenei harmónia elérésére. Az aranymetszés a zenei kompozíciók kialakításában is fellelhető, például Bartók Béla és Kodály Zoltán munkáiban is.
A költészetről is elmondhatjuk, hogy már az ókorban szabályokat állított fel a verssorok kialakítására. Ismert volt az időmértékes verselés, de a magyar nyelvben a középkortól az ütemhangsúlyos verselés is. A modern kor költői (Edgar Allan Poe, Stéphane Mallarmé, Charles Baudelaire) is elismerik a matematika szükségességét a verselésben. A nyelvnek van egy logikai, komputerizált oldala, de van egy biológiai, pszichikai, társadalmi oldala is. A vers nem fordítható matematikai formulára. A drámairodalom is alkalmaz bizonyos matematikai számításokat a darab részeinek megtervezésében. A táncművészetben a lépések szabályok szerint történnek. A tánc térbeli levezetésében, az egyéni vagy csoportos táncnál is geometrikus modelleket követnek, azért, hogy esztétikai hatást érjenek el.
Az ember az, aki felfedezi a természetben is a szépet. Ugyanígy felfedezi a matematikai összefüggéseket a természetben, és képletekbe foglalja azokat. A természetben megtalálható a szimmetria és a spirál is, ezek egyaránt leírhatók a matematika nyelvén. A méhek például szabályos hatszögűre képezik a méz tárolására szükséges edényeket, valamint az organikus mikróvilágban is szabályos szerkezeteket figyeltek meg.
Visszatérve a művészet világába, arra gondolok, hogy Worringer német művészettörténész szerint az ember alkotási módszere az idők folyamán hol absztrakt (geometrikus), hol természetközeli (realista) volt, és ezek a korszakok váltakoztak. Az absztrakt forma biztosította a rendet az ember számára a világgal való konfrontációban. Ha korunk tudósainak álláspontját akarjuk látni a matematika és művészet kapcsolatáról, akkor Solomon Marcus, romániai matematikustól tudunk meg a legtöbbet (A. B. Bejan: Interjú Solomon Marcus matematikussal). Ő együttműködött más országok tudósaival, szervezeteivel, és meggyőződése, hogy az átjárhatóság a kultúra különböző részei között egy természetes folyamat, ami mindig is létezett. De ez ma már kötelező is. A haladás feltételezi a tudásformák (tudományok, művészetek) egymásra való hatását, közreműködését. Az egyes tudományok egyre összetettebbekké válnak, és a továbbfejlődéshez igénybe veszik más tudományok eredményeit is. Korunk tudósai, például Jean Piaget hangsúlyozta a tudományok kölcsönhatását, Werner Heisenberg is úgy látta, hogy figyelni kell a rész és az egész kapcsolatára.
Solomon Marcus, a matematikai nyelvészet egyik úttörője sikeresen alkalmazott matematikai modelleket a drámairodalomban és a poétikában is, de foglalkozott formális nyelvekkel, az orvosi diagnózisok nyelvével, valamint a gépi fordítás problémáival is. Bevezette a kontextuális nyelvet, amivel a szöveg elemezhetővé válik. Megkülönböztetett algebrai és topológikus modellt: az algebrai modell lefordítható más nyelvekre, nem veszít információtartalmából, de a versfordítás (topológikus) már korlátokba ütközik. A képzőművészetek közötti átjárás is gyakorlattá vált korunkban. Például a 20. század elején az építészet és képzőművészet közel került egymáshoz. Itt az is figyelembe kell venni, hogy a képzőművészetben kialakult az absztrakt szemléleti mód, ami rokonítja az építészet nyelvezetével. A képzőművészetben megjelent a konstruktivista stílus, ami közelítette az építészeti felfogáshoz. De ugyanakkor az építészet számára ihlető forrás lehet a festők struktúraszervezési kísérletezése. A film, ami a 20. században vált tömegeket megmozgató művészetté, felhasználja a zene és a képzőművészet tanulságait.
A képzőművészet ágainak egymásra gyakorolt hatása is megfigyelhető, bár ezek a hatások a régi művészetekben is léteztek. Ma sok szobrász színezi szobrait, amit a görögök is műveltek. A kerámiában, az időjárásnak ellenálló anyagok felhasználásával szobrokat, térplasztikákat alkotnak a művészek. Ugyanez történik az üveg művészetében is. A művészek nemcsak ipari formákat, használati tárgyakat terveznek, hanem szobrászati alkotásokat is. A művészek textilanyagokból is alkotnak plasztikákat, szobrokat.
Úgy gondolom, ezek a példák igazolják, hogy a tudományok és művészetek gyakorolják az átjárást, a kulturális merészséget, amelynek segítségével gazdagabbá teszik korunkat, az ember életminőségét. Sokan kimutatták, hogy a matematikusok és költők igazából rokonlelkek abban az értelemben, hogy nagy gondolatsűrűséggel dolgoznak. A matematikus Bólyai János egy képlettel új világot alkotott, József Attila pedig a Nem én kiáltok című vers költői gondolataival az emberi lehetőségek sokaságát tárta elénk:
„Légy a fűszálon a kicsi él
S nagyobb leszel a világ tengelyénél
Hiába fürösztöd önmagadban,
Csak másban moshatod le arcodat.”








